Винеровским процессом, выходящим из нуля, называется  процесс  W(t),, удовлетворяющий следующим условиям:

1.  Все реализации  процесса W(t) непрерывны и ;

2. Для любого p = 2, 3, … значений параметров   его приращения  ,...,  независимы;

 3.Случайная величина  имеет нормальное распределение с параметрами , где  – коэффициент диффузии винеровского процесса или его интенсивность.

Таким образом, плотность распределения сл. величины  равна    ,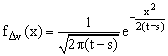

Случайный процесс  называется стандартным винеровским процессом, его интенсивность равна единице.

В определении винеровского процесса можно условие  заменить на условие , и тогда получим определение винеровского процесса, выходящего из точки x.

Зафиксируем n произвольных точек  . Случайный вектор  получается из вектора приращений  невырожденным линейным преобразованием с  матрицей A:  ,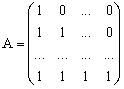

то есть   , но так как , возможно соотношение    , и обратная матрица  имеет вид 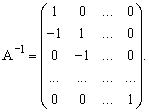    Отсюда, следуя общей теории построения законов распределения функций сл. величин, зная плотность распределения сл. величины

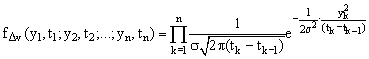, получим плотность распределения сл. величины W

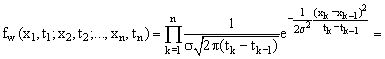
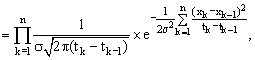 а это плотность многомерного нормального распределения с нулевым математическим ожиданием и ковариационной матрицей , равной  .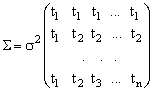

Ковариационная матрица n-мерного  нормального распределения  сл. вектора  размерности   k имеет вид:

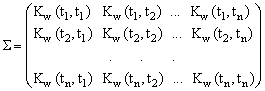. Каждая компонента матрицы Σ –  в свою очередь представима в виде: 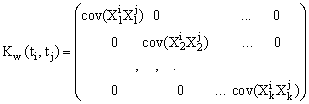.