Рассматривая симплекс-метод, мы предполагали, что задача линейного программирования является невырожденной, т.е. каждый опорный план содержит ровно  положительных компонент, где  – число ограничений в задаче. В вырожденном опорном плане число положительных компонент оказывается меньше числа ограничений: некоторые базисные переменные, соответствующие данному опорному плану, принимают нулевые значения. Используя геометрическую интерпретацию для простейшего случая, когда  (число небазисных переменных равно 2), легко отличить вырожденную задачу от невырожденной. В вырожденной задаче в одной вершине многогранника условий пересекается более двух прямых, описываемых уравнениями вида . Это значит, что одна или несколько сторон многоугольника условий стягиваются в точку.

Аналогично при  в вы­рож­денной задаче в одной вершине пересекается более 3-х плоскостей .

В предположении о невырож­ден­ности задачи находилось только одно значение 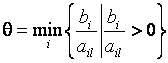, по кото­рому определялся индекс выводимого из базиса вектора условий (выводимой из числа базисных переменной). В вырожденной задаче 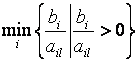 может достигаться на нескольких индек­сах сразу (для нескольких строк). В этом случае в находимом опорном плане несколько базисных переменных будут нулевыми.

Если задача линейного програм­ми­рования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Так называемое, явление зацик­ливания. Хотя в практических задачах линейного программирования зацикливание явление крайне редкое, возможность его не исключена.

Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем “незначительного” изменения вектора правых частей системы ограничений на величины , таким образом, чтобы задача стала невырож­денной, и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи.

Чаще реализуемые алгоритмы включают в себя некоторые простые правила, снижающие вероятность возникновения зацикливания или его преодоления.

Пусть переменную  необходимо сделать базисной. Рассмотрим мно­жество индексов , состоящее из тех , для которых достигается 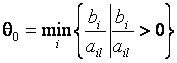. Множество индексов , для которых выполняется данное условие обозначим через . Если  состоит из одного элемента, то из базиса исключается вектор условий  (переменная  делается небазисной).

 Если  состоит более чем из одного элемента, то составляется множество , которое состоит из , на которых достигается 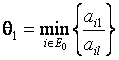. Если  состоит из одного индекса , то из базиса выводится переменная . В противном случае составляется множество  и т.д.

Практически правилом надо пользоваться, если зацикливание уже обнаружено.