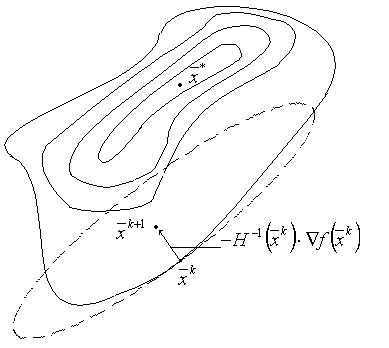
Методы второго порядка при поиске минимума используют информацию о функции и ее производных до второго порядка включительно. К этой группе относят метод Ньютона и его модификации.

В основе метода лежит квадратичная аппроксимация , которую можно получить, отбрасывая в рядах Тейлора члены третьего и более высокого порядков:

,         (1)

где  - матрица Гессе, представляющая собой квадратную матрицу вторых частных производных  в точке .

 Направление поиска  в методе Ньютона определяется следующим об­ра­зом. Если заменить в выражении (1)  на  и обозначить , то получим

,         (2)

Минимум функции  в направлении  определяется дифференциро­ва­нием  по каждой из компонент  и приравниванием к нулю полученных выражений

.                                     (3)

Это приводит к

,                                     (4)

.                                (5)

В данном случае и величина шага и направление поиска точно определены. Если  - квадратичная функция (выпуклая вниз), то для достижения минимума достаточно одного шага.

Но в общем случае нелинейной функции  за один шаг минимум не достигается. Поэтому итерационную формулу (5) обычно приводят к виду:

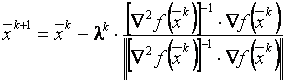,                             (6)

где - параметр длины шага, или к виду

.              (7)

Направление поиска определяется вектором  .

Итерационный процесс (6) или (7) продолжается до тех пор, пока не будет выполнен некоторый критерий останова.

Критерий, гарантирующий сходимость метода Ньютона в предположении, что функция  дважды дифференцируема, заключается в том, что матрица  должна быть положительно определенной.

Иногда определенную сложность вызывает вычисление на каждом шаге матрицы . Тогда вместо метода Ньютона используют его модификацию. Суть модифицированного метода Ньютона заключается в том, что при достаточно хорошем начальном приближении вычисляется матрица  и в дальнейшем на всех итерациях вместо  используется . Очередные приближения определяются соотношением

.              (8)

Естественно, что число итераций, необходимое для достижения минимума, обычно возрастает, но в целом процесс может оказаться экономичнее.

Градиентные методы, в частности метод наискорейшего спуска, обладают линейной скоростью сходимости. Метод Ньютона обладает квадратичной скоростью сходимости.

Применение метода Ньютона оказывается очень эффективным при условии, что выполняются необходимые и достаточные условия его сходимости. Однако само исследование необходимых и достаточных условий сходимости метода в случае конкретной  может быть достаточно сложной задачей.